
The two angles can be adjacent or non-adjacent.

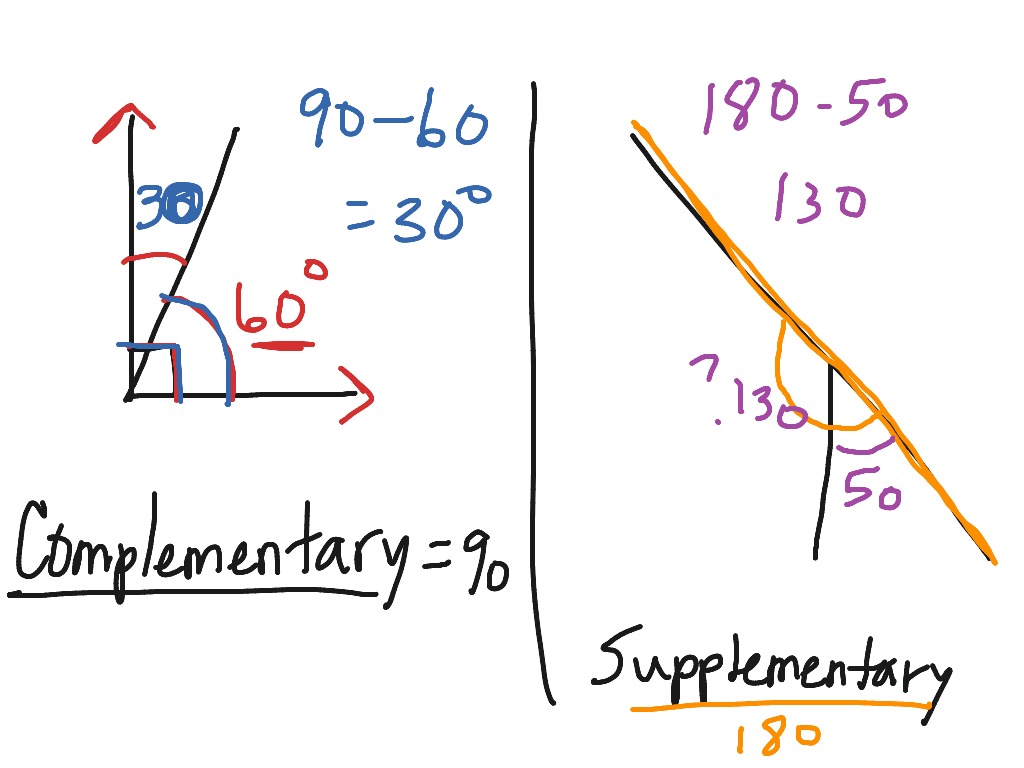
A linear pair (two angles that form a line) will always be supplementary. If one angle is known, its supplementary angle can be found by subtracting the measure. If one angle is known, its supplementary angle can be found by subtracting the measure of its angle from 180º. Two angles are supplementary if the sum of their angles equals 180o. Sum it up: Supplementary angles are two angles whose sum is 180°. Two angles are supplementary if the sum of their angles equals 180º. Geometry & Algebra: find the value of x the find the m ABD and m DBC. Remember that linear pairs are supplementary and that 2 intersecting lines will form 4 pairs of supplementary angles. How many other linear pairs can you see in the diagram?
If two angles form a linear pair then they are supplementary.Įxample 2: the angles form a line (linear pair) therefore they are supplementaryĮxample 3: the angles can be non-adjacent as long as their sum is 180°ġ10°+ 70° = 180° The sum is 180° therefore they are supplementary.ġ and 2 form a linear pair so m 1 + m 2 = 180° therefore the angles are supplementary.A linear pair is two angles that are adjacent and form a line.You just have to remember that their sum is 180° and that any set of angles lying along a straight line will also be supplementary. when two angles are supplementary angles, they are said to be supplements of each other. When the sum of two angles is 180 o, i.e. Together, the supplementary angles form a straight line. For example, two angles, 130 o and 50 o are supplementary because their sum, 130 o + 50 o 180 o. There isn’t much to working with supplementary angles. Two angles are said to be supplementary if their sum is 180 o. The two angles lie along a straight line, so they are supplementary. Vertical and supplementary angles Stock Photo any angles that form a straight line add up to 180, angles on a straight Supplementary angles are in which. Angles 1 and 2 are referred to as supplements. In other words, if, A n g l e 1 + A n g l e 2 180 angles 1 and 2 are supplementary. Give one pair of supplementary angles and one pair of vertical angles shown in the figure below. (a) Supplementary angles: and 2 4 6 8 (b) Vertical angles: - and 5 /7 13 m. When supplementary angles are combined, they make a straight angle (180 degrees). Homework help starts here Math Geometry Q&A Library Give one pair of supplementary angles and one pair of vertical angles shown in the figure below.

These angles, therefore, form a straight line when joined together. When two lines intersect each other we get 4 pairs of supplementary angles. In the figure, the angles lie along line \(m\). Supplementary angles in geometry are angles whose sum is 180 degrees.
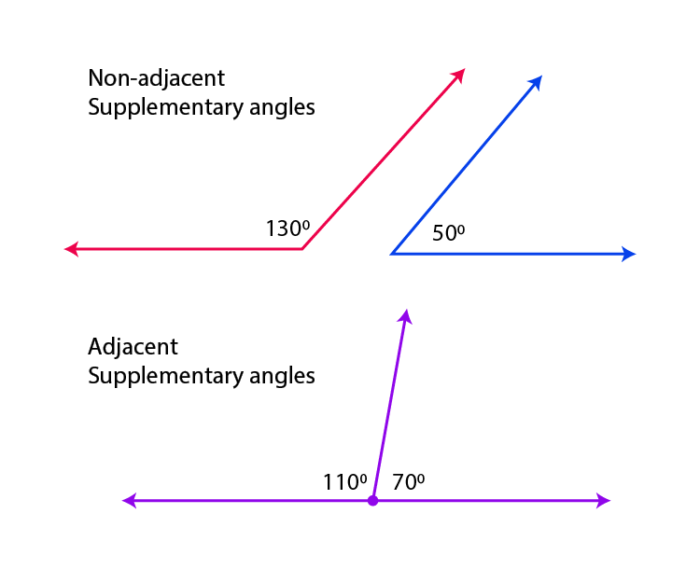
Let’s look at a few examples of how you would work with the concept of supplementary angles. Since straight angles have measures of 180°, the angles are supplementary.Įxample problems with supplementary angles The angles with measures \(a\)° and \(b\)° lie along a straight line. supplementary angles 90 +90 180 supplementary angles 40+140 180. In the image below, you see one of the common ways in which supplementary angles come up.


 0 kommentar(er)
0 kommentar(er)
